Data Flow Analysis：Applications

Overview

What is Data Flow Analysis ?

How application-specific Data flows on CFG with safe approximation.

分析算法感兴趣的数据如何流经控制流图。

  • CFG
    • Nodes (Basic Blocks) 基本块
    • Edges (Control Flow) 控制流
    • CFG(a program) 整个程序
  • Safe Approximation

safe approximation for different purposes 不同的分析目的，对于safe有不同的定义:

  • Must Analysis：Under Approximation
  • May Analysis: Over Approximation

相同点：这两种目的往往殊途同归地达到Soundness。

不同的目的对应了不同的手段：1. Data Abstraction 2. Approximation Strategies i.e. transfer functions & control flow handling.

Preliminaries for Data Flow Analysis

Input & Output States

Definition:

$IN[s]\ OUT[s]$ stand for input & output states of program points i.e. before and after executing the IR statements $s$ respectively.

e.g.:

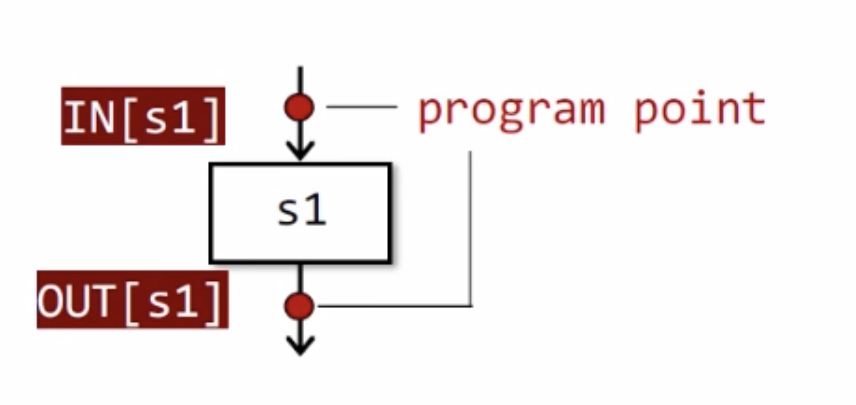
  • 下面是最简单的程序点的示意图。包括：
    1. $s_1$的输入/输出状态
    2. $s_1$的语句
    3. 程序点，包括状态信息
IMG_5B9834796776-1.jpeg

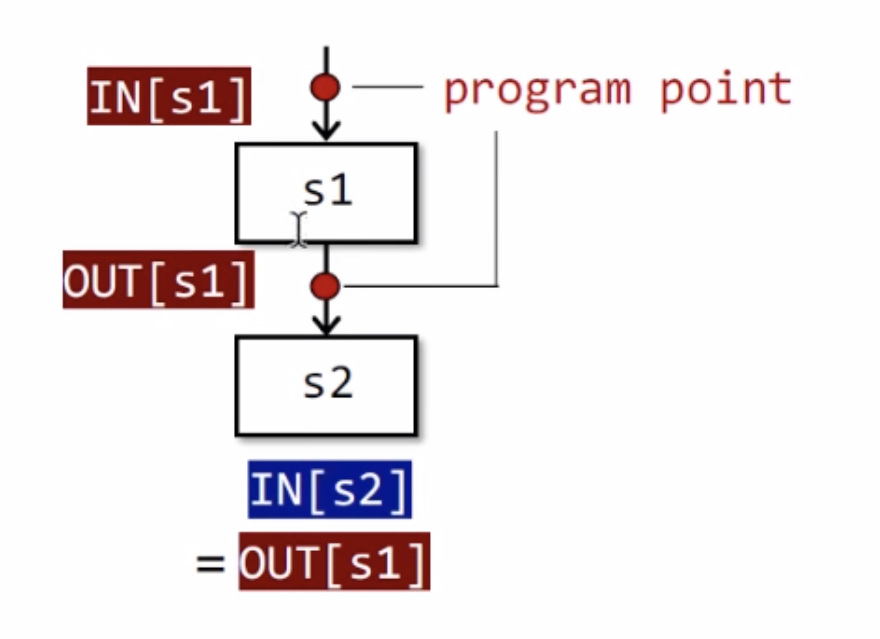
  • 语句之间的状态关系1：

    下面表示两个顺序的语句之间状态关系。

    即，$s_2$的输入是$s_1$的输出

    $IN[s_2]=OUT[s_1]$

IMG_1264.jpg

  • 带有控制流的语句间的状态关系1：

    右图表示了一种分支语句的状态关系

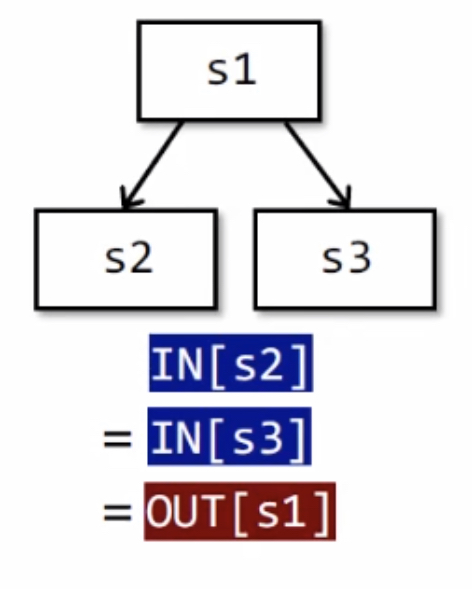
IMG_39DFBE1DA174-1.jpeg

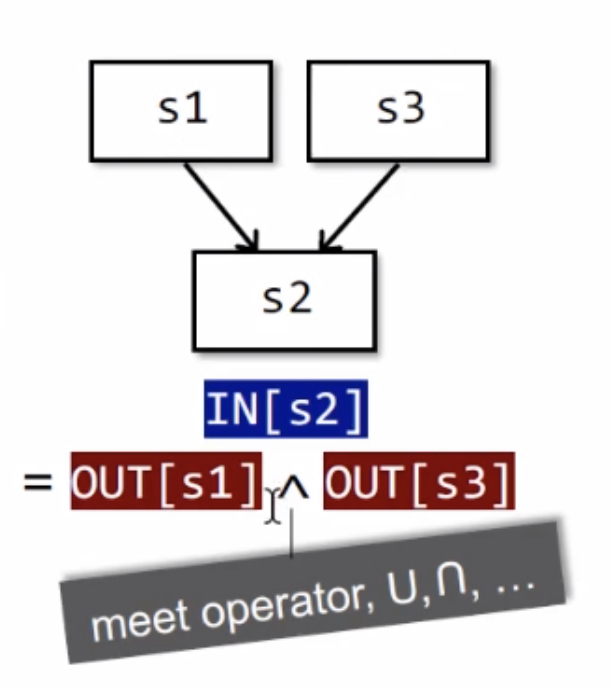
  • 带有控制流的语句间的状态关系2：

    下图是分支合并语句的状态关系，引入了操作符$\wedge$，表示语句分支的合并 IMG_1266.jpg

Domain 值域

In each data-flow analysis application, we associate with every program point a data-flow value that represents abstraction of the set of all possible program states that can be observed for that point.

data-flow value: Abstraction of the set of all possible program states that can be observed for that point.

于是，我们把 data flow value在一个程序中可能取值的集合称作 Domain.

Data flow analysis: another perspective

Data-flow analysis is to find a solution to a set of safe-approximation-directed constraints on the $IN[s]$ and $OUT[s]$, for all statements $s$.

  • constraints
    • transfer functions
    • flow of control
  • solution
    • related data flow value for each program points of statement $s$.

Notations for Transfer Functions’s Constrains

  • Forward Analysis

$OUT[s] = f_s(IN[s])$

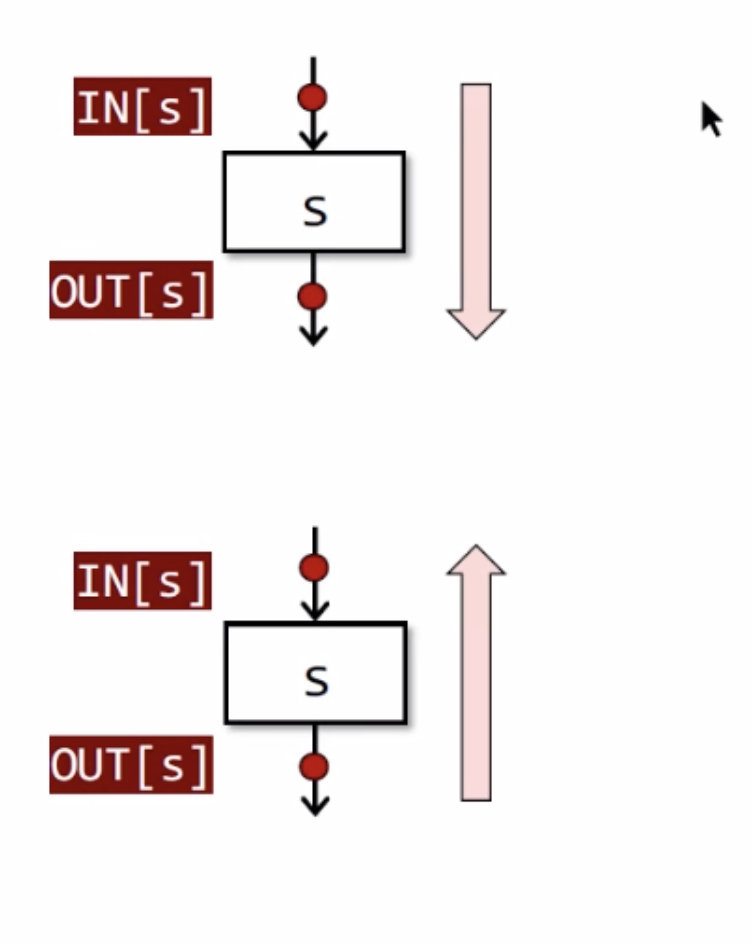
IMG_6B0F10640944-1.jpeg
  • Backward Analysis

$IN[s] = f_s(OUT[s])$

Notations for Control Flow’s Constraints

  • Control flow within a BB

    $IN[s_{i+1}]=OUT[s_i], \forall i=1,2,3,…,n-1$

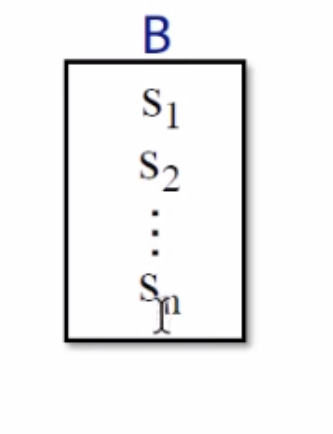
  • Control flow among BBs

    $IN[B] = IN[s_1]$

    注：BB的入口是BB第一个语句的入口

    $OUT[B]=OUT[s_n]$

    注：BB的出口是BB最后一个语句的出口

    $OUT[B] = f_B(IN[B]), f_B = f_{sn} \circ … \circ f_{s2} \circ f_{s1}$

    注：$\circ$ 表示函数的复合

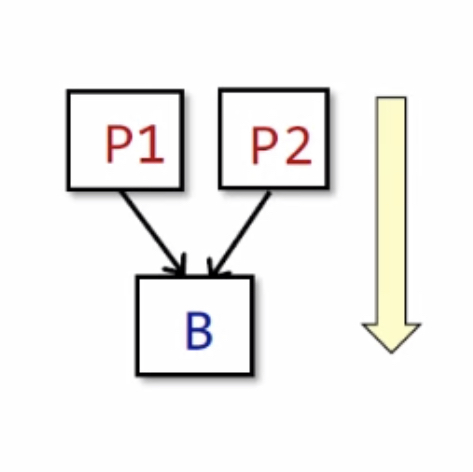
    $IN[B]=\bigwedge_{\color{red}P\\ a\ predecessor\ of\ \color{blue} B}^{} OUT[P]$

    注：分支合并B的输入等于B所有前驱节点输出状态 meet 的结果

IMG_D7917E87C141-1.jpeg IMG_2BDB7DCE680A-1.jpeg

Reaching Definitions Analysis

Definition:

A statement that assign a value to $v$. 一条对$v$的赋值语句。

Reaching Definition:

Definition of variable $v$ at program point $p$ reaches point $q$ if there is a path from p to $q$ s.t. no new definition of $v$ appears on that path.

Reaching Definition：变量$v$在从程序点$p$到程序点 $q$到过程中未被重新定义。

应用

  • Detecting possible undefined variables. 检查undefined变量

    E.g.: Introduce a dummy definition for each variable. If any at point $p$, definition of variable $v$ is dummy, then it is undefined.

    e.g.: Application in Optimization: Check if the variable

Abstraction

  • Data Flow Values / Facts

    • The definition of all the variables in a program.
    • represented by Bit Vectors

    e.g.: $D_1, D_2, D_3, …, D_{100}$ (100 definitions)

    [ 0000...0 ] <——(100 bits)

    Bit $i$ from the left represents definition $D_i$

Safe-Approximation

考虑语句：

D: v = x op y

本条语句将程序中 $v$ 的其他定义去除，其他变量的定义不受影响。

  • Transfer function 数学语言表达

    $$OUT[B] = gen_B \cup (IN[B] - kill_B)$$

    其中$gen_B$基本块$B$产生的definition的集合

    $kill_B$代表所有$B$以外基本块对$B$内变量的更改语句的集合

  • Control Flow

    • 是 Forward Analysis，算法从Entry 跑到Exit
    • 由于是 May Analysis，因此不会忽略任意一个分支

    $$IN[B] = \bigcup_{P\ a\ predecessor \ of\ B} OUT[P]$$

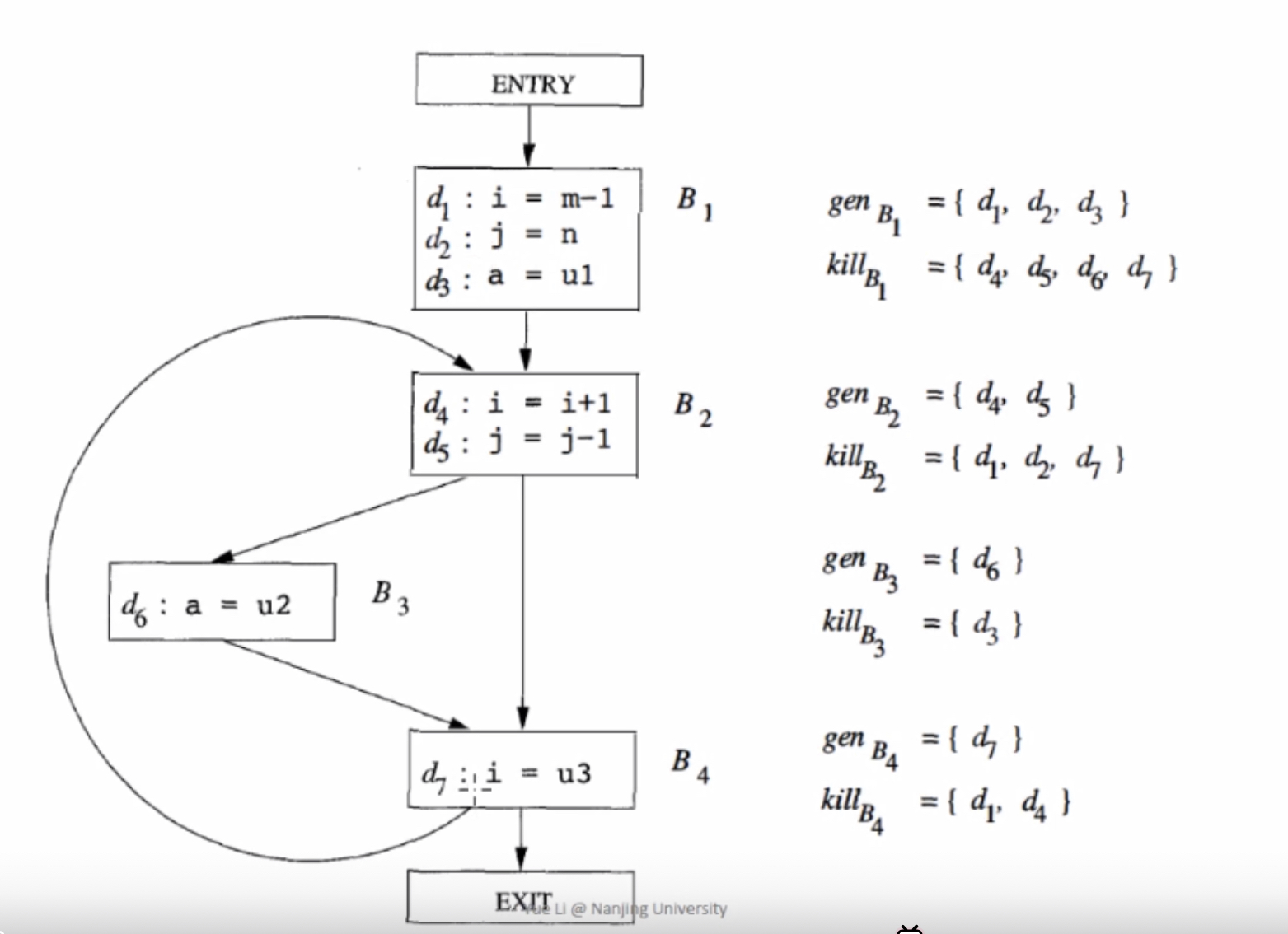
  • 下图是龙书上 $gen_B$ 和 $kill_B$ 的例子 IMG_C1B6C8D6DC93-1.jpeg

Algorithm of Reaching Definition Analysis

reaching definition algorithm

练习题

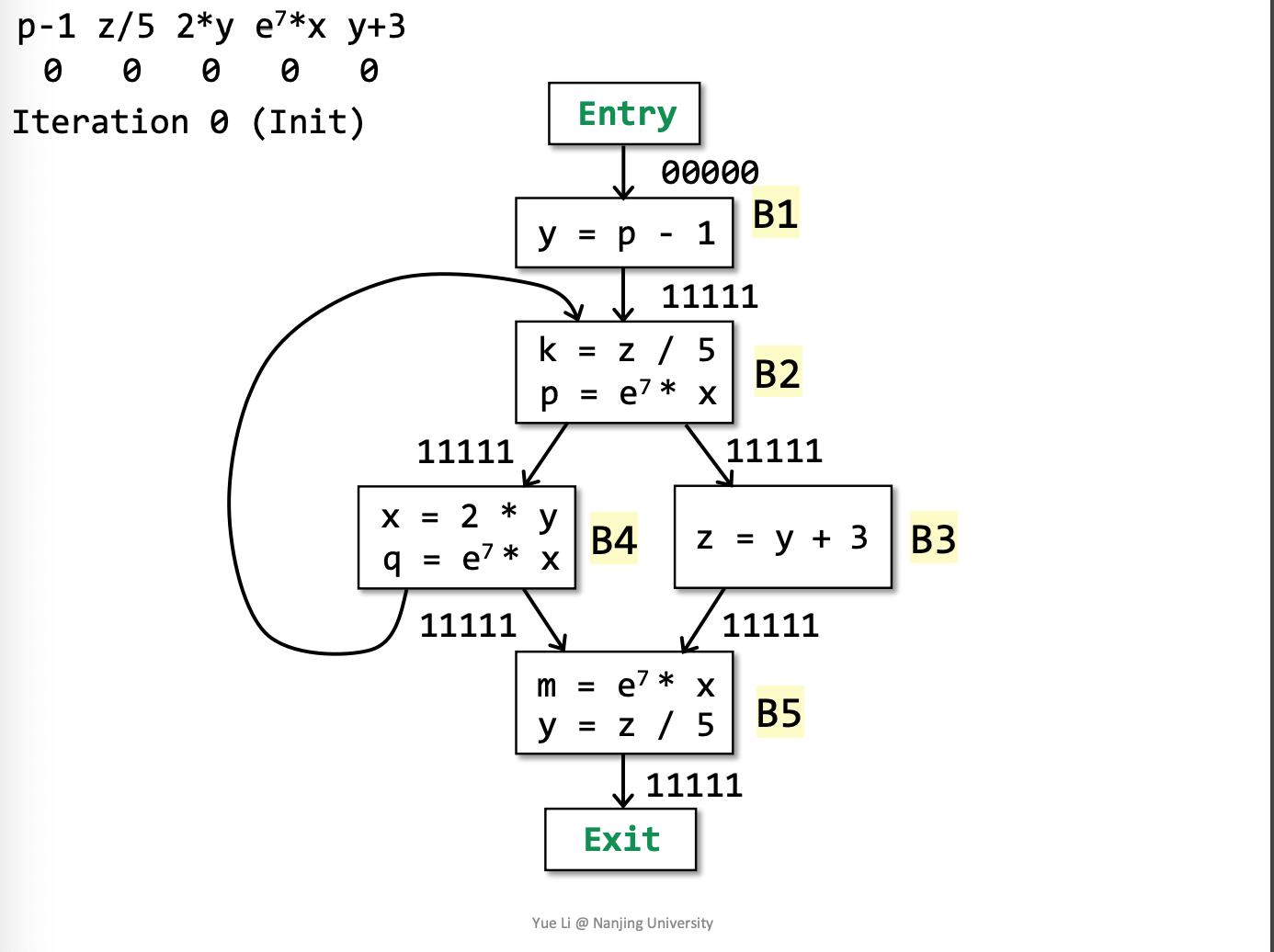
  • 练习: 对以下CFG执行 **Reaching Definition Analysis，**给出最终的$IN$和$OUT$
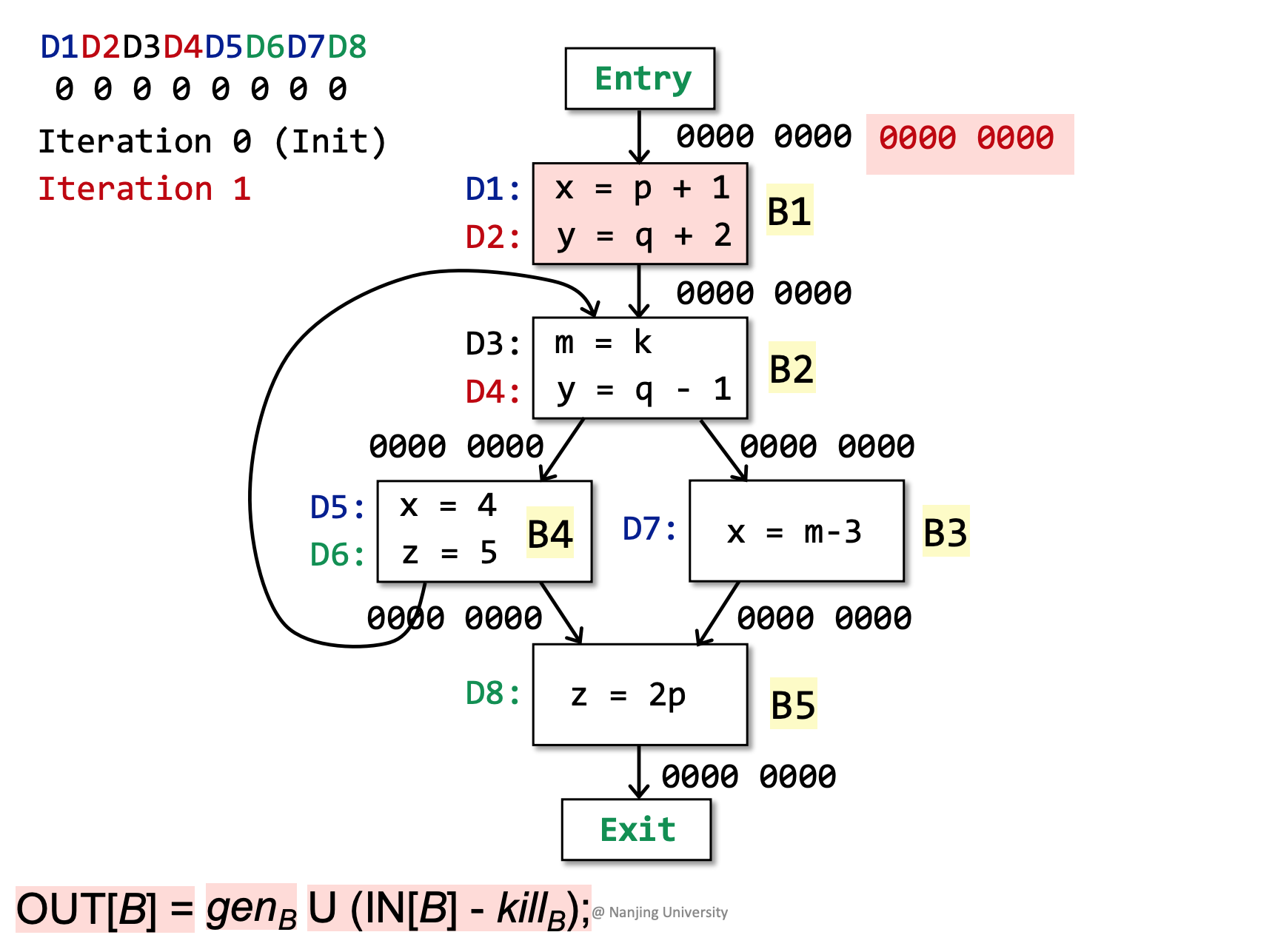
截屏2022-01-03 下午10.59.42.png

Understanding the why the loop will definitely stop （理解算法的收敛性）

  • $gen_s$ 和 $kill_s$ 是常量

  • $IN[s]$ 每次增加的因子factor（这里指Definition）要么被$kill_s$ 要么被带入$OUT[s]$

IMG_06A792AB1F78-1.jpeg
  • 于是$OUT[s]=f_s(IN[s])$ 单调不减 ($OUT[s]$要么0→1， 要么 1→1 )
  • 又由于factor本身是有限的 i.e. OUT[s]最多变成 1111…1111 就不变了。
  • 类比一下数列的单调有界准则。

Understanding the safe-approximation （理解算法安全近似性）

  • 当$OUT[s]$不再变化时，$IN[s]$是否会再次变化？

    答案是不会，由于

    $IN[B] = \bigcup_{P\ a\ predecessor \ of\ B} OUT[P]$

    所有的$IN[B]$ 取决于 $OUT[P]$ 的值，于是$IN[B]$的值不变。

    $OUT[B] = gen_B \cup (IN[B] - kill_B)$

    于是所有的 $OUT[s]$也不会改变。

练习：对以下CFG，利用Reaching Definition Analysis，计算各个BB最终的$IN$和$OUT$

Live Variable Analysis

Definition:

Live variable analysis tells whether the value of variable $v$ at program point $p$ could be used along some path in CFG starting at $p$. If so, $v$ is live at $p$；otherwise，$v$ is dead at $p$.

(这也意味着：$v$ should not be redefined before usage)

  • Application：
    • Register Allocation (寄存器分配）

Abstraction

  • Data Flow Values/Facts
    • All the variables in a program
    • Can be represented by bit vectors
      • 0: dead 1: live

Safe-Approximation

  • why forward analysis is not appropriate for live variable analysis?

    • Assume we use forward analysis strategy, information of using should be propagate backward whenever a statement use $v$ is reached, which costs a lot.
    • 我们利用反证法的思想：假设我们使用前向分析，变量使用的信息将会被向后传播，那还不如直接进行后向分析来的方便。

  • According to the definition, the live variable should be a may analysis.

  • understand the term ‘live’: determine whether the variable $v$ in some register $R$ is live, or should we delete the value of $v$ in $R$, at the point of $IN[B]$?

    If Yes, $IN[B] = {v}$ else $IN[B] = {}$

由于是may analysis，Control Flow通过以下式子给出

$$ OUT[B] = \bigcup_{S\ is\ a successor\ of\ B} IN[S] $$

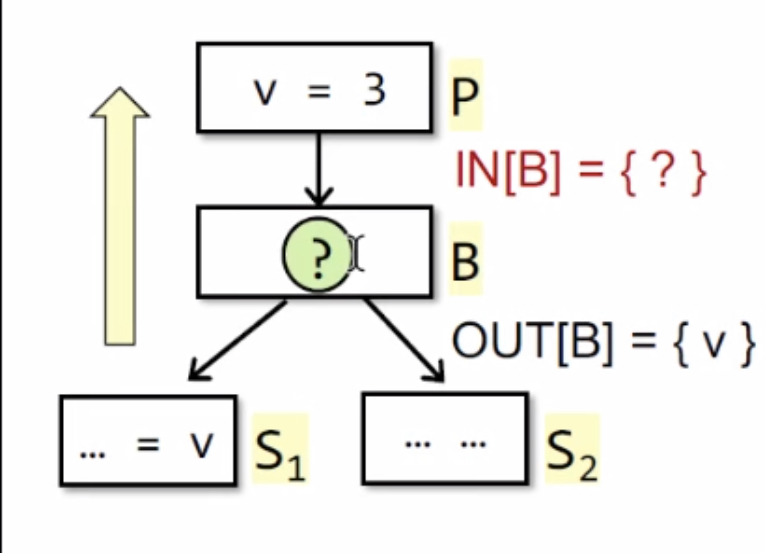
IMG_1276.jpg

  • 盲人摸象：我们通过以下一组练习，探索所有B关于$v$的表达式之情况，来探索出 Transfer Function

    练习：根据上图的CFG，并给定$OUT[B] = {v}$，考虑以下$B$的表达式对应的$IN[B]$

    1. k = n 2. k = v 3. v = v - 1 4. v = 2; k = v 5. k = v; v = 2 6. v = 2

  • *答案：

    1. k = n: 由于没有涉及到$v$，根据原则，寄存器$R$不应删去$v$的值，因此$IN[B] = {v}$
    2. k = v : 由于涉及到use $v$，我们不应该删去$v$的值，因此$IN[B] = {v}$
    3. v = v - 1 : 这题看似是对 $v$进行了新的定义，但是就语义而言，将会先对$v$的旧值进行读取，于是我们没有必要 kill 掉$v$，因此 $IN[B] = {v}$
    4. v = 2; k = v ：这题看似使用了 $v$，但是先kill掉了$v$的定义，因此 $IN[B] = {}$
    5. k = v; v = 2 ：*正好与上题相反，先对$v$进行了use，因此$IN[B] = {v}$
    6. v = 2 ：$v$被kill掉，显然 $IN[b] = {v}$

  • 先来回答集合中那些增减的量

    • $use_B$：集合中在任何use先于define的变量集合。
    • $def_B$：集合中任何define先于use的变量集合。

  • 于是，我们可以摸索出一个 Transfer Function

    $$ IN[B] = use_B \cup(OUT[B]-def_B) $$

  • 思考：kill $def_B$ 和 union $use_B$ 的顺序是否影响算法的正确性？

    结论：不影响，直觉上来看，根据$def_B$和$use_B$的定义，$def_B \cap use_b = \phi$

    不失严谨地，我们可以证明这个性质：

    【推论】

    已知 $def_B \cap use_b = \phi$， $IN[B] = use_B \cup(OUT[B]-def_B) = (OUT[B] \cup use_B) - def_B$ 成立

    【证明】

    考虑集合运算公式： $(B-A) \cup C = (B\cup C) - (A - C)$

    我们有：

    $$ IN[B] = use_B \cup(OUT[B]-def_B) = (use_B \cup OUT[B]) - (def_B - use_B) $$

    由于 $def_B \cap use_b = \phi$，于是有$def_B-use_B =def_B$

    那么，

    $$ (use_B \cup OUT[B]) - (def_B - use_B)=(use_B \cup OUT[B]) - def_B $$

    $\blacksquare$

Algorithm

按照Reaching Definition Analysis的框架，不难得到。但是有一点不同：

由于是BackWard Analysis，从Exit节点开始遍历。

live variable algorithm

练习题

  • 练习: 对以下CFG执行 **Reaching Definition Analysis，**给出最终的$IN$和$OUT$
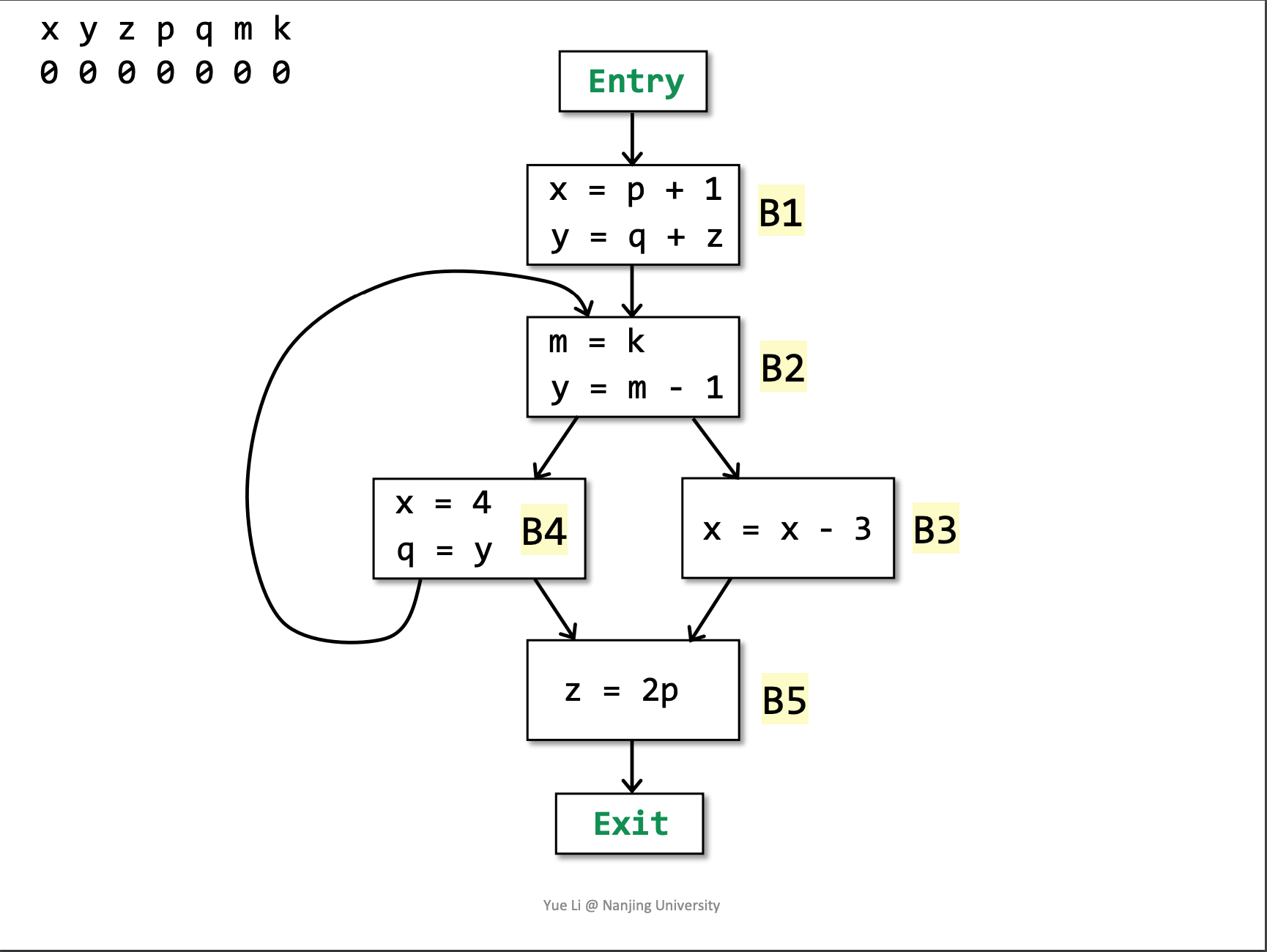
截屏2022-01-03 下午11.28.34.png

Available Expression Analysis

Definition

Available:

An expression x op y is available at program point $p$ if

  1. All paths from the entry to p must pass through the evaluation of x op y
  2. After the last evaluation of x op y, there is no redefinition of x or y

Explanation:

  • 这里的redefinition表明：原本的结果失效，我们可以需要更改 x op y 的结果值
  • available expression的信息可以用于检查全局相同的子表达式
    • 比如，在某几个BB中表达式的值不变，我们就可以删去那个表达式，直接将缓存的结果赋给变量，优化掉重复计算。

Abstraction

  • All the expressions in a program
  • Also represented by Bit Vectors

Safe-Approximation

注：

  1. As the definition illustrated, the available expression analysis ought to be a MUST ANALYSIS.
  2. As we are analyzing expression in all control flows, forward analysis is preferred to bring the information.

Transfer Function

$gen_B$: Any expression included by $B$ to be involved.

$kill_B$: Any expression contains variables redefined in $B$ to be excluded.

我们可以得到Transfer Function：

$$ OUT[B] = gen_B \cup (IN[B]-kill_B) $$

Control Flows

For it is a must analysis, control flow ought to defined by:

$$ IN[B] = \bigcap_{P\ predecessor\ of\ B } OUT[P] $$

Algorithm

available expression algorithm
  • 练习: 对以下CFG执行 **Reaching Definition Analysis，**给出最终的$IN$和$OUT$
截屏2022-01-04 下午2.09.17.png

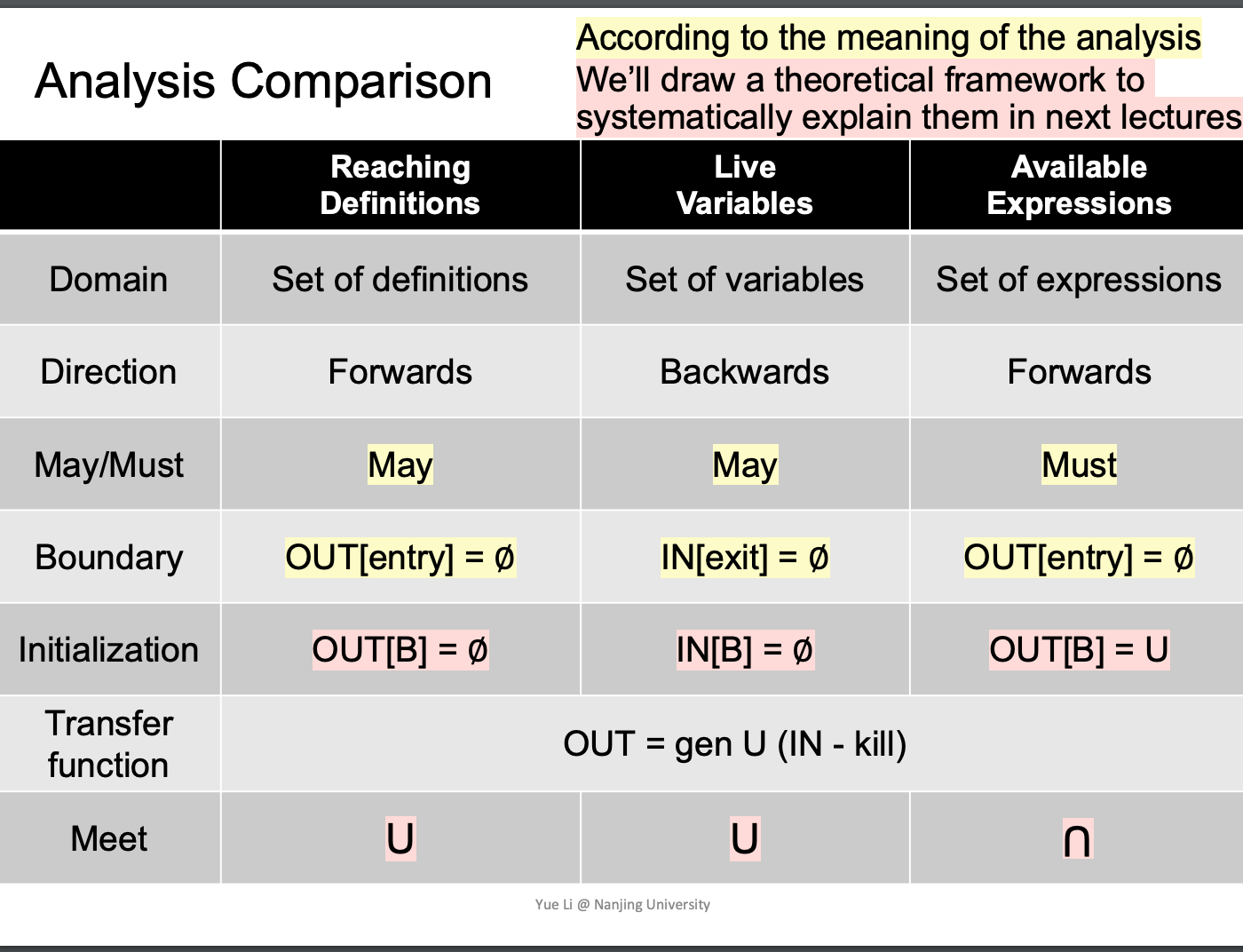
Comparison for three data flow analysis

练习：根据以上的内容，填写下表（不要参考上面的材料）

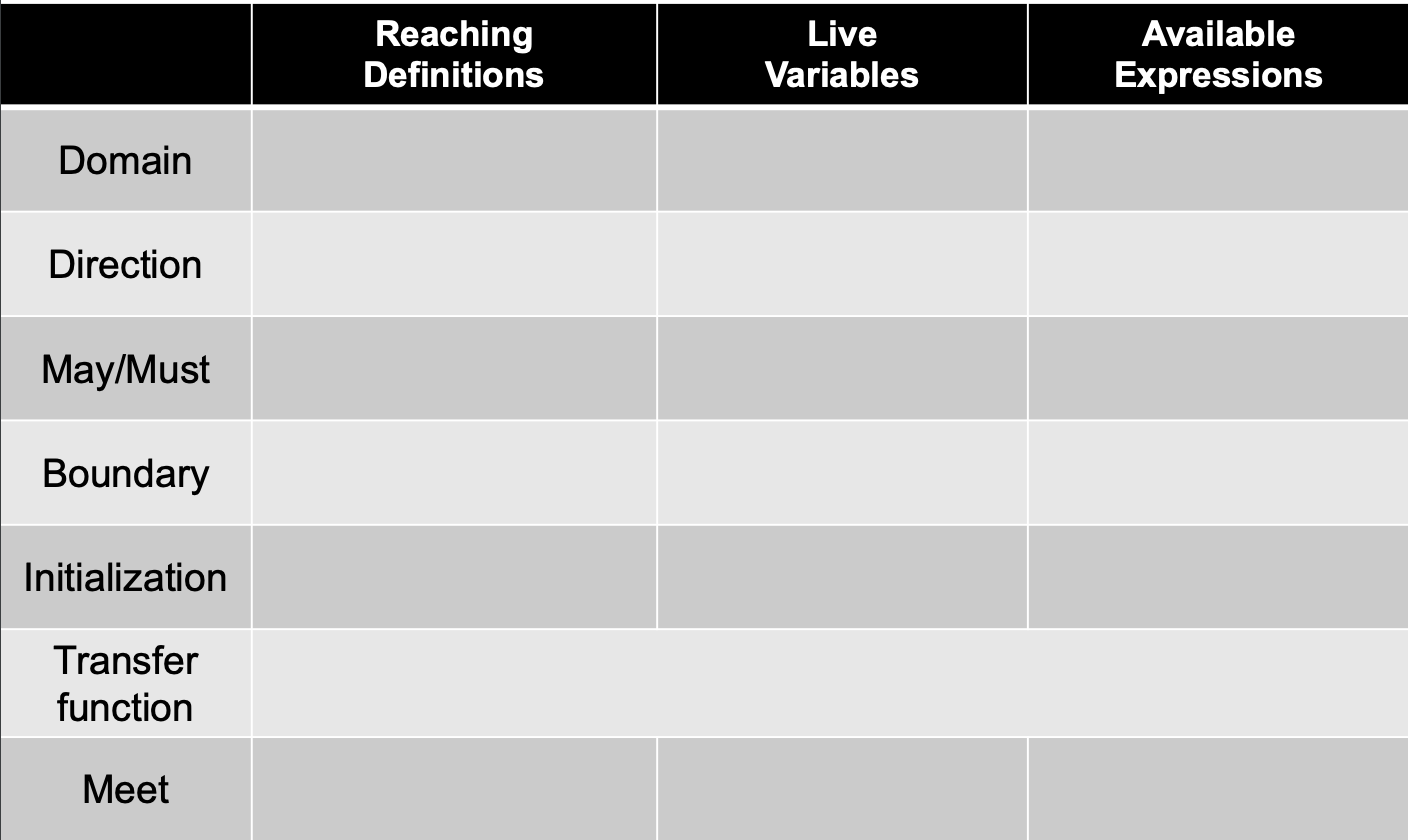
截屏2022-01-04 下午2.13.06.png
  • 答案：
截屏2022-01-04 下午2.19.11.png