Data Flow Analysis: Foundations

在应用篇的所有算法，都可以看作是 Iterative Algorithm

现在，我们从形式化 Formal的角度来审视这些算法：

A Functional View of Iterative Algorithm

• (Define)Given a CFG i.e.: a program with k nodes, the iterative algorithm updates $OUT[n]$ for every node n in each iteration.

• (Domain)Assume the domain of the values in data flow analysis is $V$, then we can define a K-tuple

  $$ (OUT[n_1],OUT[n_2],…,OUT[n_k]) $$

  as an element of set $(V_1 \times V_2 \times … \times V_k)$ denoted as $V^k$, to hold the values of the analysis after each iteration.

• (Action)Each iteration can be considered as taking an action to map an element of $V^k$ to a new element of $V^k$, through applying the transfer functions and control-flow handling, abstracted as a function $F: V^k \to V^k$

• (Convergence)Then the algorithm outputs a series of k-tuples iteratively util a k-tuple is the same as the last one in 2 consecutive iterations.

问题

• 算法一定会收敛到不动点吗？或者说算法能得到一个解吗？
• 若能收敛，那么不动点唯一吗？如果多于一个，那么如何找到最优解？
• 算法何时可以收敛到不动点？我们何时可以得到一个解？

数学基础1 Maths Basis I

Partial Order 偏序

We define poset as a pair$(P,\sqsubseteq )$ where $\sqsubseteq$ is a binary relation that defines a partial ordering over $P$, and $\sqsubseteq$ has following properties:

1. Reflexivity 自反性，$\forall x \in P, x \sqsubseteq x$
2. Antisymmetry 反自反性，$\forall x,y \in P,x \sqsubseteq y \wedge y\sqsubseteq x \Rightarrow x=y$
3. Transitivity 传递性，$\forall x,y,z \in P,x \sqsubseteq y \wedge y\sqsubseteq z \Rightarrow x \sqsubseteq z$

例：A $(S,\sqsubseteq$) is a poset where $S$ is the power set(幂集) of set $\{a,b,c\}$ and $\sqsubseteq$ represents $\subseteq$(subset).

注：这个例子还反应了poset元素的一个原则，要么 $a \sqsubseteq b$，要么$b \sqsubseteq a$，要么b与a是不可比较（incomparable，如右图没有箭头连接的集合）的，不存在骑墙者。

Upper and Lower Bounds 上界与下界

Definition:

Given a poset $(P,\sqsubseteq)$ and its subset $S$ that $S \subseteq P$, we say that $u \in P$ is an upper bound of $S$, if $\forall x \in S, x \sqsubseteq u$.

注1：以上定义用除了上界元素以外的子集定义上界，回想一下函数极值点的定义。

注2：$x \sqsubseteq u \Leftrightarrow x \leftarrow u$ ，且 $u \in P, x \in S$

Similarly, $l \in P$ is a lower bound of $S$, if $\forall x \in S, l \sqsubseteq x$.

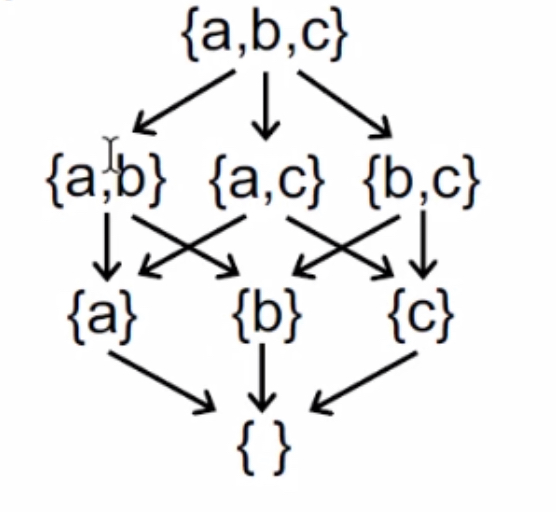
例子：求子集$S$的上界与下界

• 答案：

upper bound: $\{a,b,c \}$

lower bound: $\{ \}$

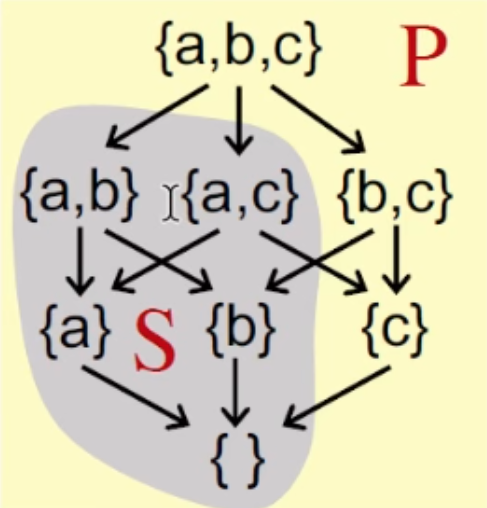
Least upper bound 上确界 (also called LUB or join ) of $S$, written $\sqcup S$,

if for every upper bound of $S$, say $u$, $\sqcup S \sqsubseteq u$

Greatest lower bound 下确界 (GLB or meet) of $S$, written $\sqcap S$,

if for every lower bound of $S$, say $u$, $\sqcap S \sqsubseteq u$

注：上下界是一个集合，而上下确界是单个元素

**例子：**求子集$S$的上确界与下确界

• 答案：

  $S$的上界：$\{ \{a,b,c\}, \{a,b\}\}$

  那么$S$的上确界：$\{a,b\}$

  S的下界：$\{ \{\}\}$

  S的下确界：$\{\}$

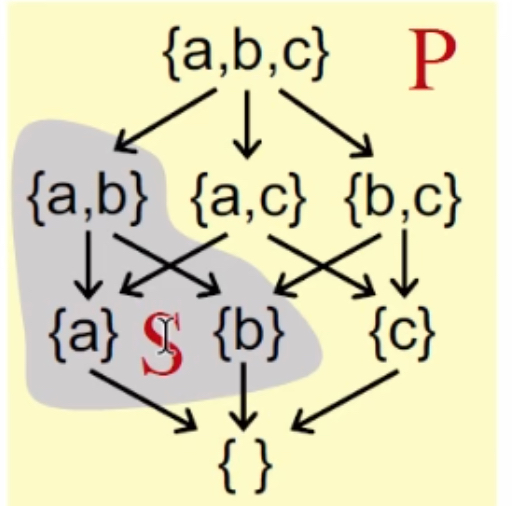
Special Cases 特殊情况

Usually, if $S$ contains only two elements $a$ and $b$ ($S={a,b}$), then

$\color{red}\sqcup S$ can be written in $\color{red}a \sqcup b$ ( join of $a$ and $b$)

$\color{blue}\sqcap S$ can be written in $\color{blue}a \sqcap b$ ( meet of $a$ and $b$)

注：略微抽象，结合上面的例子进行理解。

Properties of bounds 界的性质

• 不是所有的牛奶都叫特仑苏，不是所有的poset都有 LUB 或 GLB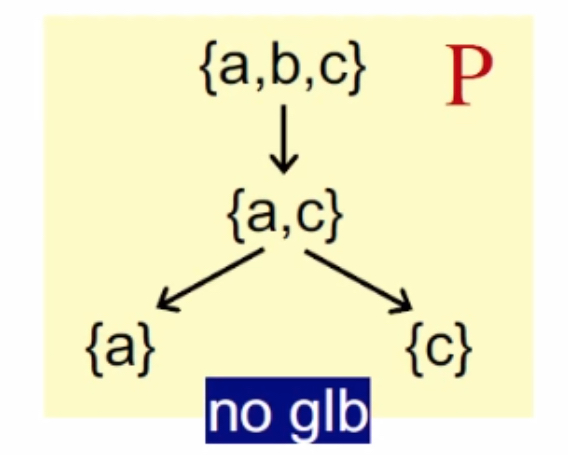 唯一性：

• 若一个poset的子集$S$存在LUB或GLB，那么这个子集的LUB和GLB将是唯一的

  • 【证明】

    反证法：

    要证明结论，不妨假设偏序集$(P，\sqsubseteq)$的子集是$S$ s.t. $S$存在 GLB

    且满足存在两个相异的GLB $g_1$ 和 $g_2$。

    由于 $g_1$ , $g_2$ $\in S$，因此，由 GLB的定义可知：$g_1 \sqsubseteq g_2$ 且 $g_2 \sqsubseteq g_1$。

    而根据poset的Antisymmetry性质可知：$\forall x,y \in P,x \sqsubseteq y \wedge y\sqsubseteq x \Rightarrow x=y$

    而$g_1$ 和 $g_2$相异，这与Antisymmetry性质矛盾。

    于是，GLB是唯一的。

    同理可证，LUB也是唯一的。

    $\blacksquare$

Lattice 格

Definition:

Given a poset $(P,\sqsubseteq)$, $\forall a, b \in P$, if $a \sqcup b$ and $a\sqcap b$ exist, then $(P,\sqsubseteq)$ is called a lattice.

Intuition:

A poset is a lattice if every pair of its elements has a LUB and a GLB.

例1：$(S,\sqsubseteq)$ is a lattice where $S$ is a set of integers and $\sqsubseteq$ represents $\le$.

⭕ The $\sqcup$ equals to $max\{a,b\}$

The $\sqcap$ equals to $min\{a,b\}$

例2：$(S,\sqsubseteq)$ is not a lattice where $S$ is a set of strings , $\sqsubseteq$ stand for the substring relation.

❌“pin” $\sqcup$ “sin” does not exists.

例3：A $(S,\sqsubseteq$) is a lattice where $S$ is the power set(幂集) of set $\{a,b,c\}$ and $\sqsubseteq$ represents $\subseteq$(subset).

⭕ The $\sqcup$ equals to $\cup$

The $\sqcap$ equals to $\cap$

Semi-lattice 半格

Definition:

Given a poset $(P,\sqsubseteq)$, $\forall a, b \in P$,

if only exists $a \sqcup b$, it is called join semi-lattice.

if only exists $a\sqcap b$, it is called meet semi-lattice.

*Complete lattice

Definition:

Given a lattice $(P,\sqsubseteq)$ , for arbitrary subset of $S$ of $P$, if $\sqcup S$ and $\sqcap S$ exists, then $(P,\sqsubseteq)$ is called a complete lattice.

Intuition:

All subsets of a lattice have a LUB and GLB

例1：$(S,\sqsubseteq)$ is not a complete lattice where $S$ is a set of integers and $\sqsubseteq$ represents $\le$.

❌ For a subset $S^+$ including all positive integers, it has no $\sqcup S^+ (+\infin)$

*例2：A $(S,\sqsubseteq$) is a complete lattice where $S$ is the power set(幂集) of set $\{a,b,c\}$ and $\sqsubseteq$ represents $\subseteq$(subset).

⭕ The $\sqcup$ equals to $\cup$

The $\sqcap$ equals to $\cap$ Properties:

• Every complete lattice $(P,\sqsubseteq)$ has:

  • a greatest element $\top = \sqcup P$ called top.
  • a least element $\bot = \sqcap P$ called bottom.

• Every finite lattice (P is finite) is a complete lattice. 有穷格一定是完全格.

• A complete lattice is not bound to be a finite lattice 完全格不一定是有穷集合

  • e.g. : $\{ x\in R\ |\ 0\le x \le1\}$ is a complete lattice with infinite numbers of elements

Product Lattice

Recall Cartesian product 复习一下笛卡尔积: e.g. Given set $A=\{a,b\}$ and $B=\{1,2,3\} $, $A \times B = \{(a,1),(a,2),(a,3),(b,1),(b,2),(b,3)\}$

Definition:

Given lattices $L_1 = (P_1, \sqsubseteq_1)$, $L_2 = (P_2, \sqsubseteq_2)$, … , $L_n = (P_n, \sqsubseteq_n)$,

if $\forall i$, $(P_n, \sqsubseteq_n)$ has $\sqcup_i$ (least upper bound) and $\sqcap_i$ (greatest lower bound), then

we can have a product lattice $L^n = (P, \sqsubseteq)$ that is defined by:

• $P = P_1 \times P_2 \times … \times P_n$
• $(x_1, … , x_n) \sqsubseteq (y_1, …, y_n) \Leftrightarrow (x_1 \sqsubseteq y_1) \wedge (x_2 \sqsubseteq y_2) \wedge … \wedge (x_n \sqsubseteq y_n)$
  • 注：右边即同时满足这些关系
• $(x_1, … , x_n) \sqcup (y_1 , …, y_n) =(x_1 \sqcup y_1 ,…,x_n \sqcup y_n)$
• $(x_1, … , x_n) \sqcap (y_1 , …, y_n) =(x_1 \sqcap y_1 ,…,x_n \sqcap y_n)$

Properties:

• A product lattice is a lattice.

  注：本身性质不变，仍是格

• If a product lattice $L^n$ is a product of complete (and finite) lattices, then $L^n$ is also complete (and finite).

  注：作积，完全性与有限性不变

Data Flow Analysis Framework via Lattice

以格为基础的数据流分析框架

Framework in a formal meaning

A data flow analysis framework $\color{black}(\color{red}D,\color{green}L,\color{blue}F \color{black})$ consists of:

• $\color{red}D$: a direction of data flow: forwards or backwards
• $\color{green}L$: a lattice including domain of the values $V$ and a meet $\sqcap$ or join $\sqcup$ operator
• $\color{blue} F$: a family of transfer functions i.e. $f: V → V$

Data flow analysis can be seen as iteratively applying transfer functions and meet/join operations on the value of a lattice.

接下来，就要回答开篇的问题

算法一定会收敛到不动点吗？或者说算法能得到一个解吗？ 若能收敛，那么不动点唯一吗？如果多于一个，那么如何找到最优解？ 算法何时可以收敛到不动点？我们何时可以得到一个解？

算法一定可以达到不动点吗？

复习一下，应用篇关于函数单调性的理解。

我们不动点是所有不动点中最好的吗？又如何定义“最好”？

数学基础2 Math Basis II

Monotonicity 单调性

definition:

A function $f$: $L\rightarrow L$ ( $L$ is a lattice) is monotonic if $\forall x, y \in L, x \sqsubseteq y \Rightarrow f(x) \sqsubseteq f(y)$

Fixed-Point Theorem 不动点定理

Given a complete lattice $(L, \sqsubseteq)$, if

1. $f: L \rightarrow L$ is monotonic and
2. $L$ is finite, then

the least fixed point of f can be found by iterating

$f(\bot), f(f(\bot)), …, f^k(\bot)$ until a fixed point is reached.

1. 存在性 2. 最小性*

注1：回忆单调有界准则

注2：这里的最小性是相对于

1. 起始点为$\bot$

2. 关于$f$ 迭代的“目标”为May（注意和Forward 和 Backward 无关）

的情况而言（回忆May和Must的区别），

因此这里叫做**最近性（离起始点最近的收敛点）**更好。

• 接下来，证明这个定理。

  【证明】

  先证存在性：

  根据$\bot$和$f$的定义，我们有：

  $$ \bot \sqsubseteq f(\bot) $$

  又由于 $f$是单调的，我们有：

  $$ f(\bot) \sqsubseteq f( f(\bot)) = f^2(\bot) $$

  同样地，不停地重复迭代应用 $f$，我们有：

  $$ \bot \sqsubseteq f(\bot) \sqsubseteq f^2(\bot)\sqsubseteq f^3(\bot)\sqsubseteq …\sqsubseteq f^n(\bot) $$

  又由于 $L$是有限集合，并且

  $$ f(\top) =\top $$

  因此，$\exists k>0\ \ s.t.$

  $$ f^{Fix}=f^k(\bot)=f^{k+1} (\bot) $$

  因此，不动点存在。

  $\blacksquare$

  再证明最小不动点，反证法：

  假设在不动点$f^k(\bot)$的基础上，还有一个不动点 $x$ i.e $x = f(x)$

  根据 $\bot$ 的定义有： $\bot \sqsubseteq x$

  数学归纳法：

  • 起始条件：因为$f$是单调的，我们有：

  $$ f(\bot) \sqsubseteq f(x) $$

  • 假设 $f^i(\bot) \sqsubseteq f^i(x)$ 成立
  • 由于$f$单调，于是$f^{i+1}(\bot) \sqsubseteq f^{i+1}(x)$

  于是由数学归纳法可知

  $$ f^i(\bot) \sqsubseteq f^i(x) $$

  因此，当$f^k(\bot) \sqsubseteq f^k(x) = x$ 时，我们有

  $$ f^{Fix} = f^k(\bot) \sqsubseteq x $$

  因此，不动点是最小的。

  $\blacksquare$

Now what we have just seen is the property (fixed point theorem) for the function on a lattice.

We cannot say our iterative algorithm also has that property unless we can relate the algorithm to the fixed point theorem, if possible.

要将我们的算法将不动点定理关联上。

Relate Iterative Algorithm to Fixed Point Theorem

Abstraction

Consider the k-tuple in Iterative Algorithm as a Product Lattice $L$

将算法中的 k元组（Bit Vector）抽象为Product Lattice.

$$ L=(P,\sqsubseteq)\ P=(P_1, P_2,…,P_n) $$

将一个一次iteration的过程抽象为函数$f:L\to L$

而整个抽象的过程可以看作复合函数$f^k$

由于Domain是Product Lattice，我们的根据其定义以及算法的行为，有以下洞见：

1. Transfer Function: $f_i: L \to L$

2. Join/Meet Function $\sqcap /\sqcup: L \times L \to L$ （注意这里的$\times$属于损失严谨性的符号滥用）

   i.e. $(x_1, … , x_n) \sqcup (y_1 , …, y_n) =(x_1 \sqcup y_1 ,…,x_n \sqcup y_n)$

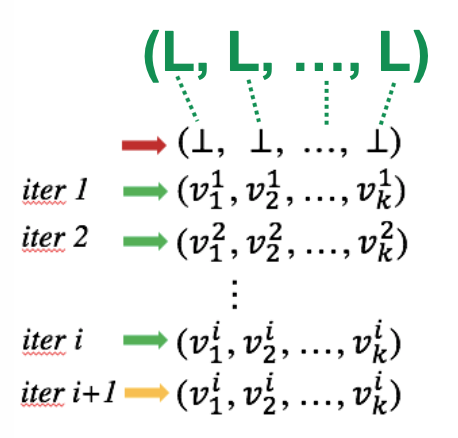
Convergence 收敛存在性

不动点定理： Given a complete lattice $(L, \sqsubseteq)$, if $f: L \rightarrow L$ is monotonic and $L$ is finite, then least fixed point of f can be found by iterating.

• Finite 有界

  由于 Product Lattice的性质：

  If a product lattice $L_p$ is a product of complete (and finite) lattices, i.e., $(L, L, …, L)$, then $L_p$ is also complete (and finite)

  因此，只要我们巧妙地构造$L$，使得$L$本身是Complete Lattice并且是Finite即可。

• Monotonic 单调

  讨论 $f:L\to L$:

  由于$f$的操作为：

  1. transfer function:

     由于$gen_B$和$kill_B$为常数，容易证明其单调性。

  2. join / meet function$\sqcup / \sqcap$:

  • 我们证明 2.的单调性

    不妨证明 $\sqcup$的单调性：

    问题：若 $\forall x,y,z \in L, x \sqsubseteq y$ , 证明 $x \sqcup y \sqsubseteq y \sqcup z$

    【证明】

    根据 $\sqcup$的定义，有 $y \sqsubseteq y \sqcup z$

    又由于 $x \sqsubseteq x \sqcup y$ 且 $x \sqsubseteq y$

    于是有 $x \sqsubseteq y = y$

    因此，$x \sqcup y \sqsubseteq y \sqcup z$

    同理可证 $\sqcap$ 也是单调的

    $\blacksquare$

于是，我们解决了前两个问题，即算法收敛性与收敛点唯一性。

（不动点定理可以一次回答前两个问题）

Performance Analysis 性能分析

第三个问题，算法何时收敛，即算法的复杂度如何？

我们拿前面幂集的图举例：

我们知道，这是一个Lattice。

假设$\top = \{a,b,c\} , \bot = \{\}$

我们定义：格的高度 $h$$\top$ 到 $\bot$ 的最多的边数，或者说，最长的路径

e.g. 右图的 $h = 3$

假设 Product Lattice $L_k$ 有 k个分量

e.g. $L_k = (L_1, L_2,…,L_k)$

考虑一种最坏情况：每个迭代只有**一个分量（满足Lattice性质）**更新，且对于所有分量，都“走”最长的路径。

容易得到：

该算法的最坏复杂度为$O(hk)$，其中$h$是格的高度，$k$是Product Lattice的分量数目。

（重要）May / Must Analysis, a lattice View

我们现在将用Lattice理论解释May 和 Must Analysis背后的原因。仍然用几个问题来鸟瞰以下这个部分

• 为何May Analysis 会找到最小不动点 / 为何Must Analysis 会找到最大不动点？
• 为何Must Analysis和May Analysis的初始化各自是那样的？

图例

⚠️逻辑绕弯警告：

以Reaching Definition Analysis为例

• 首先回忆：它是一种May Analysis
• 其次，假设我们正在分析一个程序所有可能 undefined 的变量
• 从两个极端情况讨论：

  1. 当分析算法初始化时，我们将全部的Lattice分量初始化为$\bot$。

     这说明：在起始态，认为所有的Definition都是无法到达的，即所有的Definition在所有程序点都**无效（undefined）**了。我们认为，这是Unsafe的。

     注：这个unsafe与safe的提法会有歧义，但是形式逻辑上是一致的，暂且按照课程的观点走。

  2. 当分析算法认为，所有的definition都到达了（111…111），显然，分析程序不会报 warning：xxx variable undefined 。我们认为这是Safe的。

• 而算法的运行过程就是：不断扩大Unsafe（undefined）的范围（由于是Monotonic的），直到一个最优的点（Fixed-point）。
  • 最优：1. （正确）在那一点，会存在误报undefined 情况，但是所有真正undefined 的变量都会包括进来。2. （最好）包括误报的undefined 的范围最小。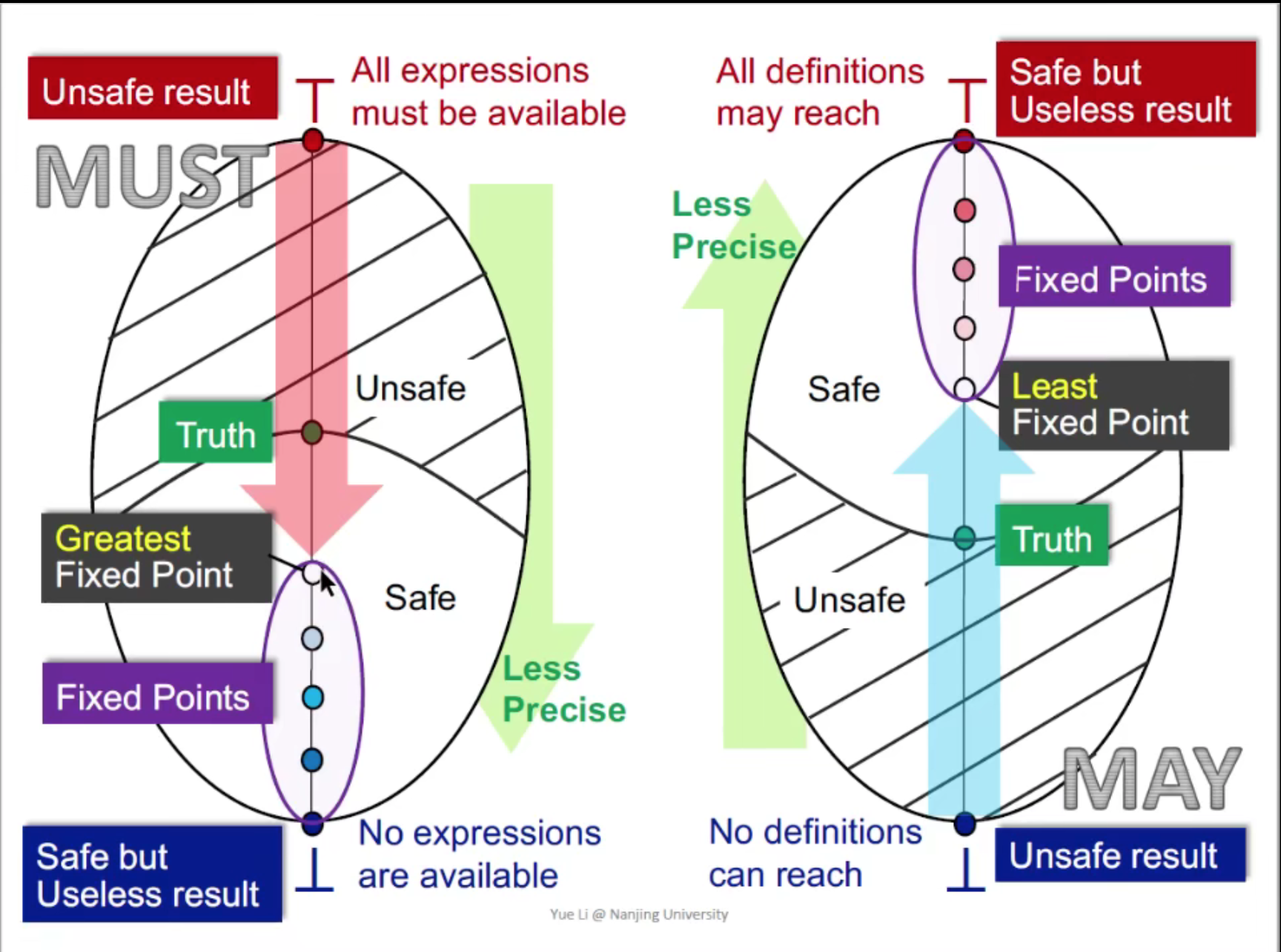 这张图很重要，建议收藏！！！

以Available Expression Analysis为例

• 首先，这是Must Analysis
• 其次，假设我们正在分析一个程序的表达式是否需要在某些BB进行重复计算。
• 极端情况：

  1. 所有的表达式都available，即 所有的表达式都不需要重复计算，我们称所有表达式都Unsafe。

     （简记：不重新计算可能造成结果错误，所以叫Unsafe）

  2. 没有表达式都available，即 所有的表达式都需要重复计算，即没有优化可能，我们称所有表达式都Safe。

• 算法运行过程：不断扩大Safe的范围（注意⚠️这一点），直到最优的点。
  • 最优：1. （正确）所有的unavailable表达式都被包含进来 2. （最好）保证本可以缓存却被排除的表达式数目最少。

总结：

• 以上两种分析算法，最终都体现了Sound的结果。
• 对于最小/大的不动点，从另一个角度来看，由于我们设计的算法本身每次迭代的操作够atomic，也就是说步子迈得足够小，于是不动点是最小/最大的。
• 由于我们transfer function和 join/meet function的合理设计，满足了不动点落在safe区域的条件

How Precise is our Solution?

我们通过介绍一些理想的模型用于对比Iterative Algorithm来衡量Precision。

（对比OS内存交换的OPT与LRU算法，以及CLRS的竞争性分析）

Meet-Over-All-Paths Solution (MOP)

• 什么是MOP？

  定义路径 $P=entry\to s_1 \to s_2 \to …\to s_i$

  对于路径$P$，定义Transfer Function $F_p=f_{s_1}\circ f_{s_2} \circ…\circ f_{s_i}$

  而$MOP[s_i]$，即将所有从$entry$ 到$s_i$的路径上的transfer function的输出，meet或join起来，找到LUB或GLB，形式化地有：

  $$ MOP[s_i] = \sqcup / \sqcap_{A\ path\ P\ from\ Entry\ to\ S_i }F_p(OUT[Entry]) $$

• MOP的局限性

  • 真实程序中，存在CFG中存在，而动态程序中不会到达的分支。 e.g. condition always true
  • 在实现过程中，MOP没有一个明确的收敛点。e.g. 无限循环

MOP vs. Iterative:以may analysis 为例

首先，分别利用表达式概括MOP过程与Iterative 的过程 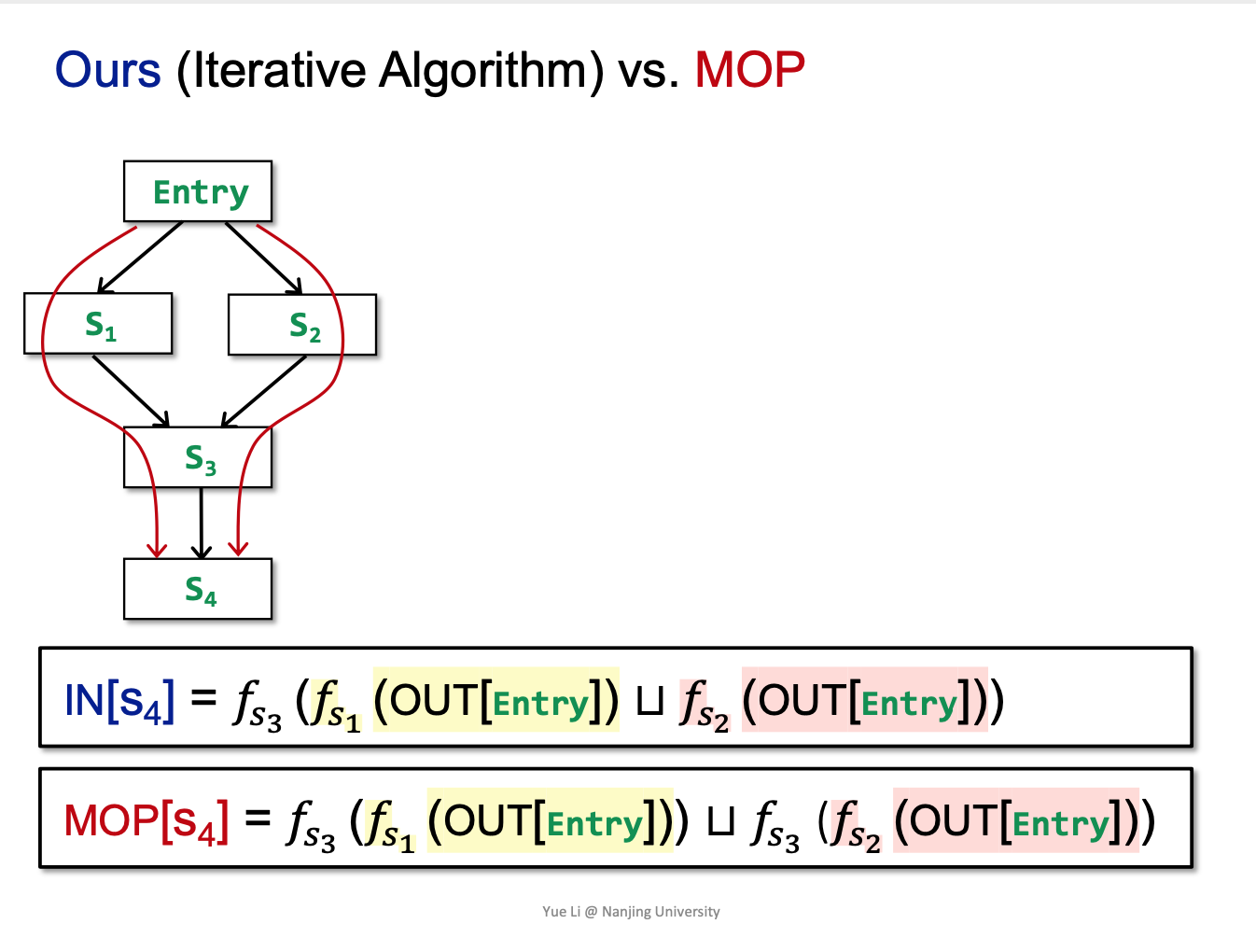形式化地：

$$ Iterative=F(x\sqcup y)\ MOP=F(x) \sqcup F(y) $$

定理：MOP比我们的方法得到的不动点更准确。

【证明】

根据$\sqcup$的定义有 $x \sqsubseteq x \sqcup y$ 以及 $y \sqsubseteq x \sqcup y$

由于$F_P$是单调的，因此有：

$F(x) \sqsubseteq F(x\sqcup y)$ 以及 $F(y) \sqsubseteq F(x\sqcup y)$

又由于

$F(x) \sqcup F(y) \sqsubseteq F(x)$

于是由传递性：

$F(x)\sqcup F(y) \sqsubseteq F(x\sqcup y)\ \ i.e.\ MOP \sqsubseteq Iterative$

根据不动点与truth点的相对关系，可知$MOP$比$Iterative$更准。

$\blacksquare$

推论：当且仅当$F_P$满足分配律（distributive），$MOP$与$Iterative$的准确度相等

形式化地，即 $F(x)\sqcup F(y) = F(x\sqcup y)$

Worklist Algorithm

对于，我们还有一些优化的手段，或者说，concrete methods to implementation。

问题：

对于Iterative Algorithm， while判断不动点时，存在冗余的计算，如何消除冗余？

Idea：

利用一个worklist来保存各个BB的状态，若某个BB已经到达不动点，就踢出worklist。

否则，就需要计算BB的所有后继节点。

Algorithm: Forward Analysis as An Example

复习要点

• Understanding Functional View of Iterative Algorithm
• Lattice and Complete Lattice
• Fixed-Point Theorem and proof
• How to summarize may and must analysis in a lattice perspective.(The picture)
• The relation between MOP and the iterative algorithm by proof.
• Worklist Algorithm